Tiny-LLM(三):实现分组查询注意力(GQA)
本节将介绍如何实现 Qwen2 中使用的 分组查询注意力(GQA):让多个 Query 头共享更少的 Key/Value 头,从而显著减少 KV 投影的内存与带宽开销(MQA 是 GQA 的极端特例,所有 Q 头共享 1 个 K/V 对)。
1 任务总览
任务细节:Tiny-LLM Week1-Day3
1.1 实现 scaled_dot_product_attention_grouped
目标:实现分组缩放点积注意力函数(GQA 的核心)。函数要支持 H_q(query 头数)是 H(key/value 头数)的整数倍的情况,通过重塑 + 广播让少量的 K/V 对被多个 Q 头共享,而不是物理重复 K/V。
实现路径:src/tiny_llm/attention.py
1.2 实现 causal mask
目标:实现一个形状为 (L, S) 的因果掩码,当 mask == "causal" 时用于屏蔽注意力中“未来”位置。掩码应在被加到 scores(softmax 之前)时把不允许的位置设为 -inf。
实现路径:src/tiny_llm/attention.py(实现 causal_mask)
1.3 实现Qwen2分组查询注意力
在 src/tiny_llm/qwen2_week1.py 中实现 Qwen2MultiHeadAttention 的前向逻辑,参考以下为代码:
1
2
3
4
5
6
7
8
9
10
x: B, L, E
q = linear(x, wq, bq) -> B, L, H_q, D
k = linear(x, wk, bk) -> B, L, H, D
v = linear(x, wv, bv) -> B, L, H, D
q = rope(q, offset=slice(0, L))
k = rope(k, offset=slice(0, L))
(transpose as needed)
x = scaled_dot_product_attention_grouped(q, k, v, scale, mask) -> B, L, H_q, D ; Do this at float32 precision
(transpose as needed)
x = linear(x, wo) -> B, L, E
2 背景知识
在深入实现分组查询注意力(GQA)之前,需要理解它与传统多头注意力(MHA)、多查询注意力(MQA)的关系,以及在自回归生成中常见的因果掩码(causal mask)的作用。
2.1 分组查询注意力(GQA)
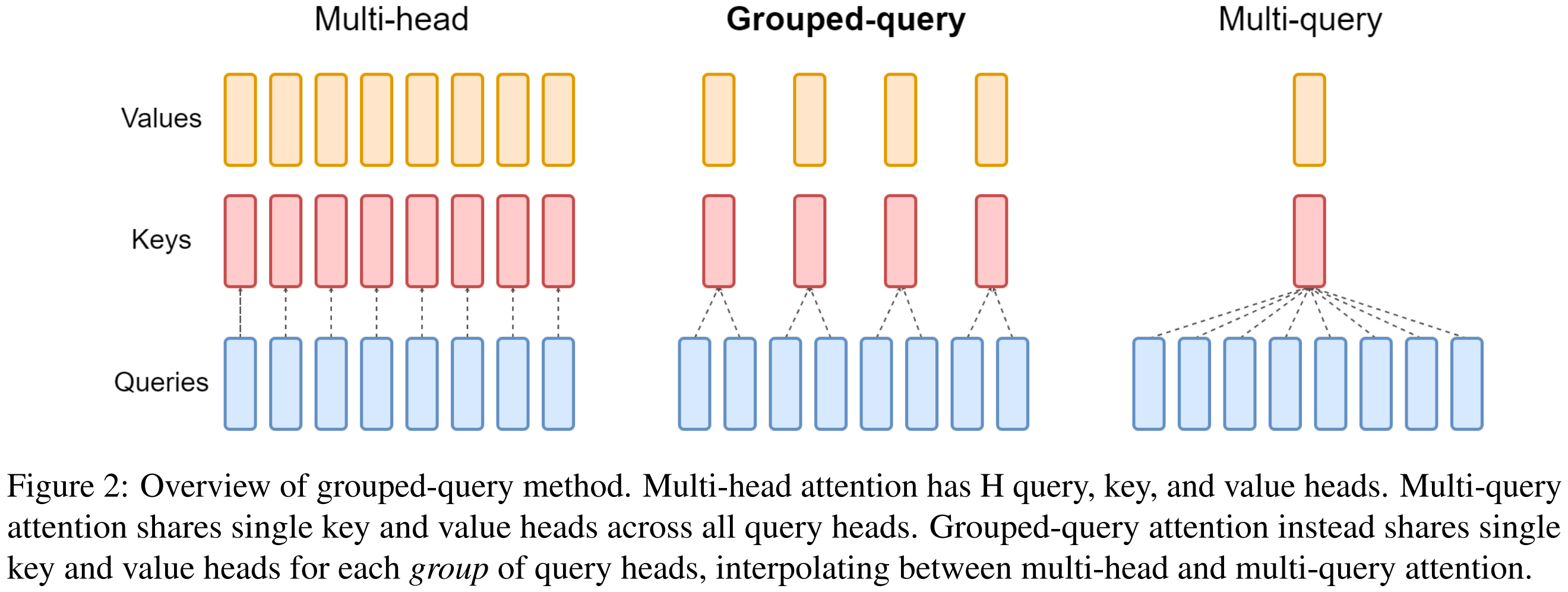
1. 多头注意力(MHA) Transformer 的注意力机制通常采用多头结构(Multi-Head Attention,MHA)。每个注意力头都有独立的 Query、Key、Value 投影矩阵,从而能在不同子空间中学习到不同的关系。然而,这种结构在推理阶段带来了显存带宽瓶颈:每个头都需要独立加载一份 KV 缓存,KV 占用和带宽消耗都随头数线性增长,严重影响生成速度。
2. 多查询注意力(MQA) 为缓解这一问题,研究者提出了多查询注意力(Multi-Query Attention, MQA)。它让所有注意力头共享同一组 Key/Value,而每个头仍保留独立的 Query。这一结构显著减少了显存读写开销,使推理速度大幅提升。但由于所有头共用相同的 K/V 表示,模型表达能力下降,训练稳定性也较差。
3. 分组查询注意力(GQA) 分组查询注意力(Grouped Query Attention, GQA)在 MHA 与 MQA 之间取得折中。它将所有 Query 头划分为若干组,每组头共享同一组 Key/Value,不同组之间仍保持独立。若组数等于头数,退化为 MHA;若只有一组,则等价于 MQA。
这种结构在速度与精度之间取得平衡,在保持接近 MHA 表现的同时显著降低 KV 缓存带宽开销。现代大模型(如 Qwen2)均采用此设计以兼顾性能与质量。
2.2 因果掩码(Causal Mask)
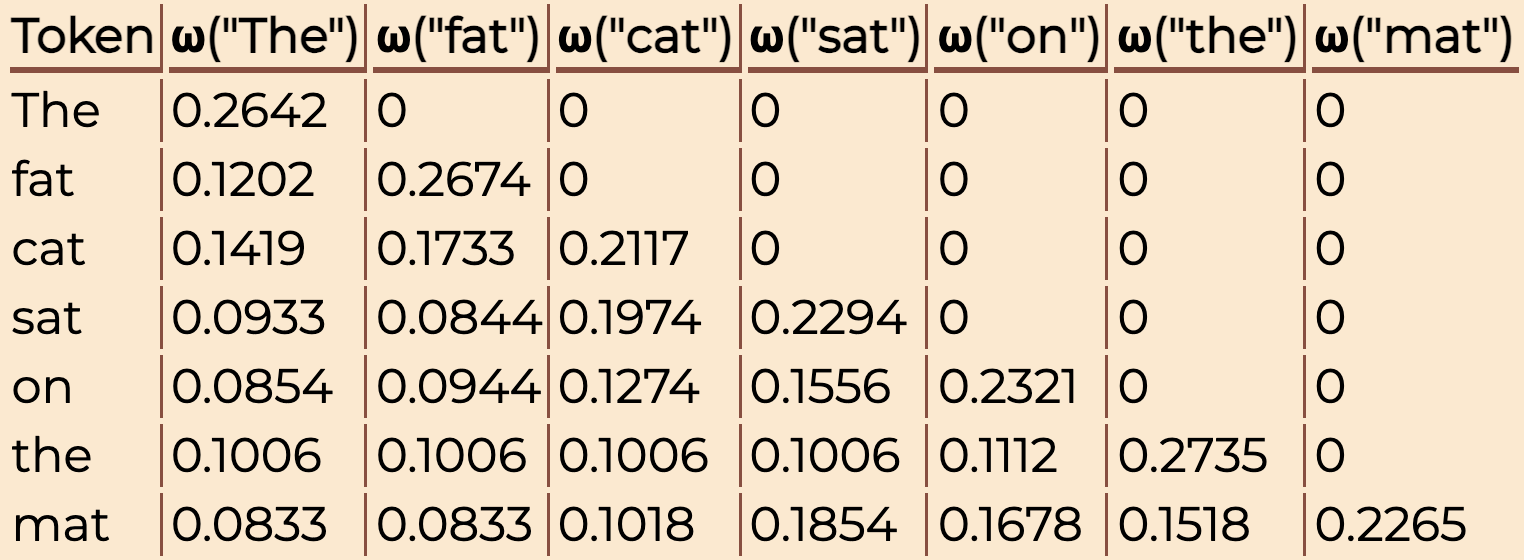
在自回归语言模型中,生成第 i 个词时不应访问未来的词,因此注意力计算需进行“因果掩码”。掩码矩阵通常是一个下三角矩阵,仅保留当前位置及之前的注意力连接,屏蔽右上方“未来词”的注意力分数。
实现时,为避免多余计算与归一化问题,常在 softmax 之前将被屏蔽部分置为 -∞,使得 softmax 后其权重自然变为 0。这种方法既高效又数值稳定,是现代 Transformer 实现的标准做法。
3 代码实现
3.1 实现 causal mask
1
2
3
4
def causal_mask(L: int, S: int, dtype: mx.Dtype) -> mx.array:
mask = mx.tril(mx.ones((L, S)), k=(S - L))
mask = mx.where(mask, mx.array(0), mx.array(-mx.inf)).astype(dtype)
return mask
mx.tril 生成一个下三角矩阵(lower-triangular),代表允许注意的位置。对角线以下为 1,以上为 0。
mx.where(mask, 0, -inf)将掩码矩阵中为 0 的部分(未来时刻)替换为 -inf。softmax(−∞)=0,确保未来的 token 权重为 0。
3.2 实现 scaled_dot_product_attention_grouped
输入形状中,h_q 是 Query 头数;h_k 是 K/V 头数(GQA 的关键区别)。n_requests 表示每组 Key/Value 被多少个 Query 头共享。
- 张量重排:为了让多个 Query 头共享同一组 K/V,需要调整张量维度。此时张量的维度结构可理解为:
(*N, 1, h_k, n_requests, L, d_k) - 注意力分数计算
- 掩码逻辑:如果传入
"causal",则自动生成因果掩码矩阵并加到分数上,被屏蔽部分会成为-inf。 - softmax + 加权求和:对应标准注意力机制
- 最后 reshape 回原始形状即可输出
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
def scaled_dot_product_attention_grouped(
query: mx.array,
key: mx.array,
value: mx.array,
scale: float | None = None,
mask: mx.array | str | None = None,
) -> mx.array:
original_shape = query.shape
h_q, L, d_k = query.shape[-3:]
h_k, S, _ = key.shape[-3:]
n_requests = h_q // h_k
N = query.shape[:-3]
query = query.reshape(*N, -1, h_k, n_requests, L, d_k)
key = key.reshape(*N, -1, h_k, 1, S, d_k)
value = value.reshape(*N, -1, h_k, 1, S, d_k)
scale_factor = scale if scale is not None else 1.0 / mx.sqrt(d_k) # scale = 1 / sqrt(d_k)
scores = mx.matmul(query, key.swapaxes(-2, -1)) * scale_factor # scores : (*N, 1, h_k, n_requests, L, S)
if mask is not None:
if mask == "causal":
mask = causal_mask(L, S, query.dtype) # mask : (L, S)
else:
mask = mx.broadcast_to(mask, (*N, h_q, L, S)) # mask : (*N, h_q, L, S)
mask = mask.reshape(*N, 1, h_k, n_requests, L, S) # mask : (*N, 1, h_k, n_requests, L, S)
scores = scores + mask
scores = mx.matmul(softmax(scores, axis=-1), value) # scores : (*N, 1, h_k, n_requests, L, d_k)
return scores.reshape(original_shape) # scores : (*N, h_q, L, d_k)
3.3 实现Qwen2分组查询注意力
类 Qwen2MultiHeadAttention 封装了完整的前向计算流程,包括线性变换、RoPE 编码、GQA 注意力计算与输出层。其中 num_heads 是 Query 头数,num_kv_heads 是 K/V 头数(通常 < num_heads)。二者的比例决定了 GQA 的分组大小。
主要步骤如下:
- 线性变换:获得标准的 Q、K、V 投影层
- 旋转位置编码(RoPE):将位置信息融入注意力中
- 调用分组注意力
- 输出线性层
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
class Qwen2MultiHeadAttention:
def __init__(
self,
hidden_size: int,
num_heads: int,
num_kv_heads: int,
wq: mx.array,
wk: mx.array,
wv: mx.array,
wo: mx.array,
bq: mx.array,
bk: mx.array,
bv: mx.array,
max_seq_len: int = 32768,
theta: int = 1000000,
):
self.hidden_size = hidden_size
self.num_heads = num_heads
self.num_kv_heads = num_kv_heads
self.d_k = hidden_size // num_heads
self.rope = RoPE(self.d_k, max_seq_len, theta, False) # use untroditional RoPE
self.wq = wq
self.wk = wk
self.wv = wv
self.wo = wo
self.bq = bq
self.bk = bk
self.bv = bv
def __call__(
self,
x: mx.array,
mask: mx.array | str | None = None,
) -> mx.array:
# 1. liear
N, L, _ = x.shape # x: (N, L, d_model)
query = (
linear(x, self.wq, self.bq) # query: (N, L, d_model)
.reshape(N, L, self.num_heads, self.d_k) # query: (N, L, h, d_k)
)
key = (
linear(x, self.wk, self.bk)
.reshape(N, L, self.num_kv_heads, self.d_k)
)
value = (
linear(x, self.wv, self.bv)
.reshape(N, L, self.num_kv_heads, self.d_k)
)
# 2. RoPE
query = self.rope(query, offset=slice(0, L))
key = self.rope(key, offset=slice(0, L))
query = query.transpose(0, 2, 1, 3) # query: (N, h, L, d_k)
key = key.transpose(0, 2, 1, 3)
value = value.transpose(0, 2, 1, 3)
# 3. scaled dot-product attention & concat
scale = 1.0 / mx.sqrt(self.d_k) # scale = 1 / sqrt(d_k)
scores = (
scaled_dot_product_attention_grouped(query, key, value, scale, mask=mask) # scores: (N, h, L, d_k)
.transpose(0, 2, 1, 3) # scores: (N, L, h, d_k)
.reshape(N, L, self.hidden_size) # scores: (N, L, d_model)
)
# 4. linear
return linear(scores, self.wo) # output: (N, L, d_model)