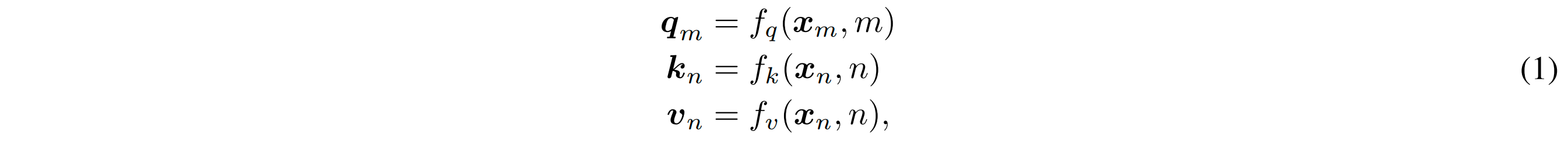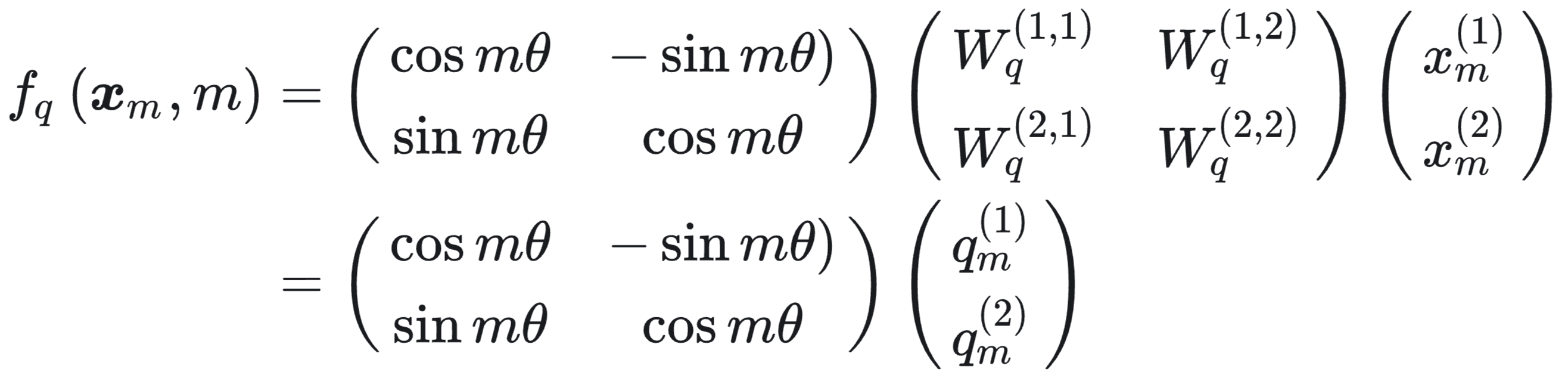Tiny-LLM(二):实现旋转位置编码(RoPE)
1 任务总览
在Transformer架构中,由于自注意力机制本身不包含位置信息,我们需要通过位置编码来为模型提供序列中token的顺序信息。本章将实现现代大语言模型广泛采用的旋转位置编码(RoPE)。
任务细节:Tiny-LLM Week1-Day2
1.1 实现传统 RoPE
在第一步中,我们需要在 src/tiny_llm/positional_encoding.py 中实现标准版本的 RoPE。
每个注意力头的维度 D 会被看作由成对的元素组成(例如 [x0, x1]、[x2, x3] 等)。每一对被当作一个复数 (x_even, x_odd),然后与对应的 cos 和 sin 频率进行旋转变换:
1
2
x'[0] = x[0] * cos - x[1] * sin
x'[1] = x[0] * sin + x[1] * cos
这样,模型就能通过旋转角度体现序列中的位置信息。
同时,我们还需要理解 offset 的概念。如果没有偏移量(offset),我们就认为序列从第 0 个 token 开始编码;如果有偏移量,比如 5..10,那就代表这个序列实际上是原始序列中第 5~9 个位置的片段,因此需要从第 5 个频率开始应用位置编码。
1.2 实现 Qwen2 风格的非传统 RoPE
在 Qwen2 模型中,RoPE 的形式略有不同。它不是成对旋转,而是将头部维度拆分为前半部分和后半部分,然后分别使用不同频率的旋转。也就是说,我们把输入向量 x 拆成 x1(前半部分)和 x2(后半部分),再执行:
1
2
output[:HALF] = x1 * cos - x2 * sin
output[HALF:] = x1 * sin + x2 * cos
这种方式可以更好地兼容多头注意力下的特征分布,让模型在保持性能的同时拥有更高的灵活性。
2 背景知识
在深入实现旋转位置编码(Rotary Position Embedding,RoPE)之前,我们需要先理解它是如何从传统位置编码演化而来的,以及它为何能更好地捕获相对位置信息并提升大模型的外推性(extrapolation)。
2.1 为什么需要位置编码?
Transformer 模型不像 RNN 那样会按顺序处理序列,因此模型本身无法“知道”一个 token 在句子中的位置。为了让模型理解序列的顺序,我们需要给每个 token 注入“位置感”,也就是位置编码(Positional Encoding)。
简单来说,词嵌入(embedding)告诉模型“是什么词”,而位置编码告诉模型“这个词在句子中在哪里”。
在经过 embedding 层后,我们得到每个 token 的词向量:xᵢ ∈ ℝᵈ 表示第 i 个 token 的 d 维向量。在计算 self-attention 之前,我们会把位置信息注入到 Q、K、V 向量中:
这里 m/n 表示位置信息。所有位置编码的设计,核心目标都是:设计一个合理的函数 f,让模型既能捕获顺序信息,又能泛化到未见过的序列长度。
2.2 传统绝对位置编码
最早的 Transformer 使用了正弦-余弦函数(Sinusoidal)生成固定的位置编码。其思路是用不同频率的 sin 和 cos 函数为不同维度的向量编码,让每个维度对应一种周期变化规律。
通俗地讲,每个位置 i 都会生成一组独特的波形模式,模型通过这些不同周期的 sin/cos 波动,就能区分“第1个词”和“第100个词”的区别。不过,这种方式存在两个问题:
- 它只能表达绝对位置(即“我是谁”),而不能表达相对距离(即“我和你差几位”)。
- 当我们希望模型在推理阶段处理比训练阶段更长的序列时,sin/cos 的周期性会让模型的泛化能力迅速下降——这就是所谓的外推性差(poor extrapolation)。
外推性是大模型中一个非常关键的能力。举个例子:如果一个模型在训练时只见过长度为 512 的文本,那么在推理时输入 2048 个 token,它可能会“迷路”,因为它从未见过那么长的上下文。
RoPE 就是为了解决这个问题:它能让模型学到位置之间的相对关系,而不是固定的绝对编号。因此,哪怕你给它更长的文本,它仍能根据“相对距离”来计算注意力,而不是依赖“第几号位置”。
2.3 旋转位置编码
论文 RoFormer: Enhanced Transformer with Rotary Position Embedding 提出了 RoPE。它的核心思想是:**用旋转操作代替位置相加操作。找到一个位置编码方式,使得 query 向量 $q_m$ 和 key 向量 $k_n$ 之间的内积能够自然地包含它们之间的相对位置信息$(m-n)$。
假设词嵌入维度为2维 $d=2$,利用二维平面上的几何性质,RoPE提出,对于query向量 $q_m$:
这实际上是一个旋转矩阵,角度 θᵢ 随位置 i 变化。这样,RoPE 把每个 token 的位置编码成一个“旋转角度”,让相对位置信息通过旋转角度差自然地体现在注意力计算中。
总的来说,RoPE 的精髓在于:
- 不再将位置编码加到 embedding 上,而是通过旋转操作融入;
- 将“绝对位置”映射为“相对角度差”;
- 让注意力计算对序列长度具有更好的外推性。
3 代码实现
RoPE 的核心是:把每一对维度 (x1, x2) 看作复数的实部与虚部,然后让它按角度 θ 做旋转:
1
2
[real] [cosθ -sinθ] [x1]
[imag] = [sinθ cosθ] [x2]
这里 $θ = pos × ω_i$,其中 $ω_i = base^{-2i/d}$,代表不同维度对应不同的旋转频率。
主要实现步骤:
构造频率矩阵:在初始化函数
__init__中,首先确定维度和频率,预先计算好cosθ、sinθ拆分:RoPE 需要把最后一维分成两部分(相当于复数的实部和虚部),有两种模式
traditional 模式:交错配对
[x0,x1], [x2,x3], ...split 模式:前半
[0:D/2)为实部,后半[D/2:D)为虚部
- 旋转:把预计算好的 cos/sin reshape 成可广播的形状,执行复数旋转
- 结果重组:把
(real, imag)拼回原维度,返回的y与输入形状相同,但每个元素都已带有位置编码。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
class RoPE:
def __init__(
self,
dims: int,
seq_len: int,
base: int = 10000,
traditional: bool = False,
):
half_dims = dims // 2
self.half_dims = half_dims
self.traditional = traditional
pos = mx.arange(seq_len) # pos = [0, 1, 2, ..., L-1]
inner = mx.arange(0, half_dims, dtype=mx.float32) / half_dims # [2i/d], i=0,...,half_dims-1
w = mx.power(base, -inner) # [1/10000^(i/half_dims)], i=0,...,half_dims-1
theta = mx.outer(pos, w) # (seq_len, half_dims)
self.cos_theta = mx.cos(theta)
self.sin_theta = mx.sin(theta)
def __call__(
self, x: mx.array, offset: list[slice] | slice | None = None
) -> mx.array:
N, S, H, D = x.shape
# apply offset
if offset is not None:
if isinstance(offset, slice):
assert offset.stop - offset.start == S, f"offset must be of length {S}"
elif isinstance(offset, list):
assert len(offset) == N, (
f"offsets must have the same length as batch size {N}"
)
for o in offset:
assert o.stop - o.start == S, f"offset must be of length {S}"
offset = mx.array([list(range(i.start, i.stop)) for i in offset])
cos_biasis = (self.cos_theta[:S, :] if offset is None else self.cos_theta[offset, :])
sin_biasis = (self.sin_theta[:S, :] if offset is None else self.sin_theta[offset, :])
# reshape x: (N, S, H, D // 2, 2)
if self.traditional: # [0, 2, 4, 6] [1, 3, 5, 7] format
x = x.reshape(N, S, H, self.half_dims, 2)
x1 = x[..., 0]
x2 = x[..., 1]
else: # [0, 1, 2, 3] [4, 5, 6, 7] format
x1 = x[..., 0 : self.half_dims]
x2 = x[..., self.half_dims : D]
# reshape basis: (N, S, 1, half_dims)
cos_biasis = cos_biasis.reshape(-1, S, 1, self.half_dims)
sin_biasis = sin_biasis.reshape(-1, S, 1, self.half_dims)
# [real; imag] = [cos -sin; sin cos] * [x1; x2]
real = mx.multiply(x1, cos_biasis) - mx.multiply(x2, sin_biasis)
imag = mx.multiply(x2, cos_biasis) + mx.multiply(x1, sin_biasis)
if self.traditional:
y = mx.stack([real, imag], axis=-1)
y = y.reshape(N, S, H, D)
else:
y = mx.concat([real, imag], axis=-1)
y = y.reshape(N, S, H, D)
return y.astype(x.dtype)