Tiny-LLM（一）：实现自注意力与多头注意力机制

在 Transformer 架构中，注意力机制是核心机制，它让模型能够动态关注输入序列的不同部分。本节将实现 Tiny-LLM 中 Transformer 的基础构建块：自注意力层和多头注意力层。

1 任务总览

核心目标：实现 Transformer 的核心组件——注意力机制

任务细节：Tiny-LLM Week1-Day1

1.1 实现缩放点积注意力函数

目标：完成基础的注意力计算单元。输入 Query、Key、Value 三个张量（形状相同），输出加权后的 Value。

核心公式： \(\text{Attention}(Q, K, V) = \text{softmax}\left(\frac{QK^T}{\sqrt{D}} + M\right) \cdot V ]\) 其中，L 表示序列长度（seq_len） ，D 表示每个 head 的维度（head_dim），M 表示可选 mask，用于禁止某些位置被关注。

实现路径：src/tiny_llm/attention.py → scaled_dot_product_attention_simple

1.2 实现多头注意力层

多头注意力本质上是：把一次注意力拆成 H 次并行的“小注意力”（每次维度更小），再把结果拼回去。

操作步骤总结如下：

步骤	操作	输出形状
1	输入 $N \times L \times E$	batch × seq_len × embed_dim
2	线性映射出 Q/K/V	仍然是 $N \times L \times (H \times D)$
3	重塑为多头：→ $N \times H \times L \times D$	每个 head 独立计算
4	调用任务一的注意力函数	输出 $N \times H \times L \times D$
5	拼回 → $N \times L \times (H \times D)$，再线性映射输出

实现路径：src/tiny_llm/attention.py → SimpleMultiHeadAttention

2 背景知识

在开始实现代码之前，理解模型的整体结构与核心算子非常重要。本章主要介绍 Transformer 的关键思想、注意力机制与多头注意力。

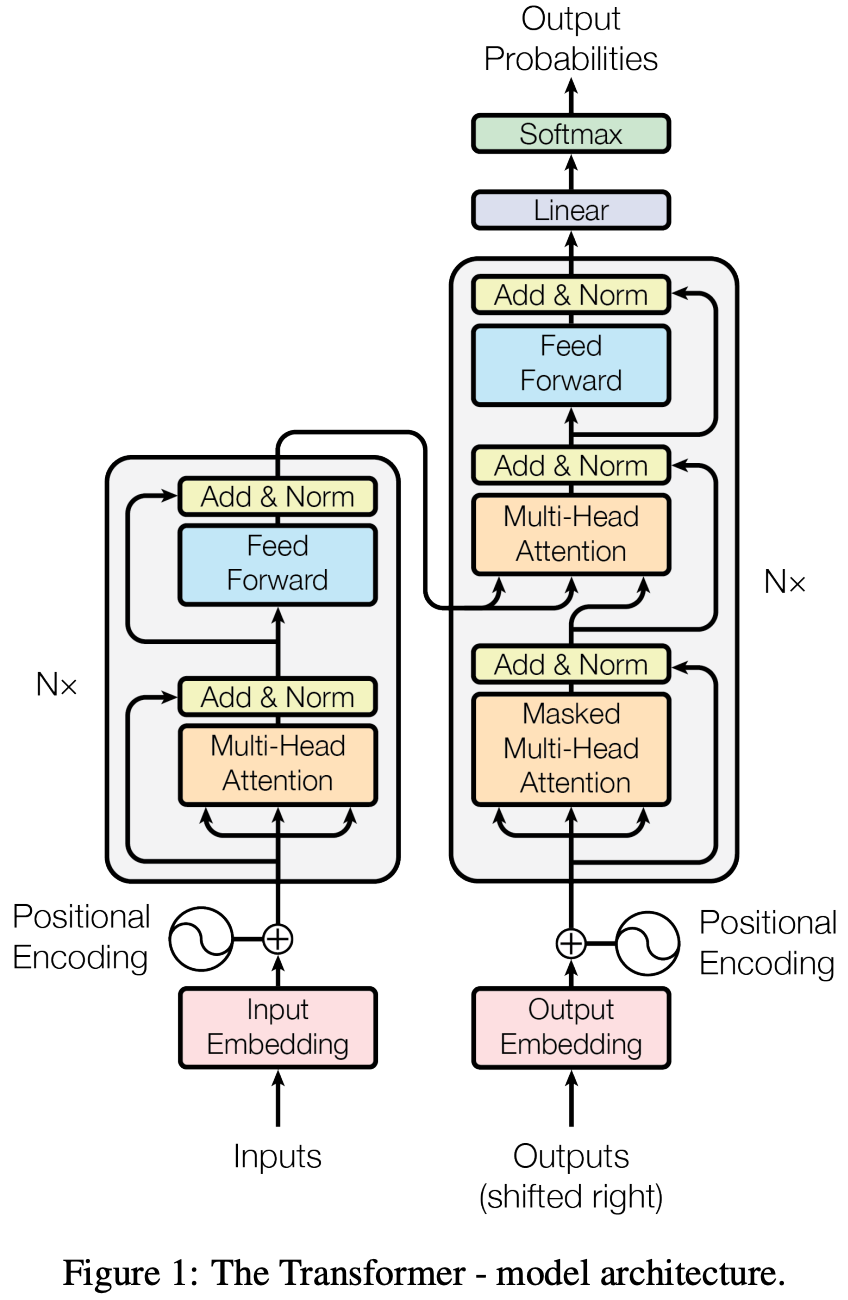
2.1 什么是 Transformer？

Transformer 是目前主流的序列模型架构（用于机器翻译、文本生成、摘要等），它的两大特点是：

• 完全基于注意力（attention）而非循环或卷积，所以能并行处理序列，训练更快。
• 灵活的编码器/解码器堆栈，可以单独用编码器、单独用解码器，或把两者组合成序列到序列（seq2seq）模型。

常见变体：

• 编码器（encoder-only）：如 BERT，擅长理解任务（分类、抽取式 QA）。
• 解码器（decoder-only）：如 GPT，擅长文本生成（自回归）。
• 编码器-解码器（encoder-decoder）：如原始 Transformer、T5，用于翻译、摘要等需要将一个序列变换成另一个序列的任务。

2.2 编码器与解码器结构

Transformer 的 encoder/decoder 都是由若干相同层叠（stack）组成，论文常用 N=6 层作为示例。每层的基本结构（encoder）：

1. 多头自注意力（Multi-Head Self-Attention）

2. 前向全连接网络（Positionwise Feed-Forward）

   每个子层外面都有残差连接 + 层归一化：output = LayerNorm(x + Sublayer(x))

Decoder 在每层中多了一个子层：对 encoder 输出的多头注意力（encoder–decoder attention），并且 decoder 的自注意力会做因果掩码，避免看到未来 token。

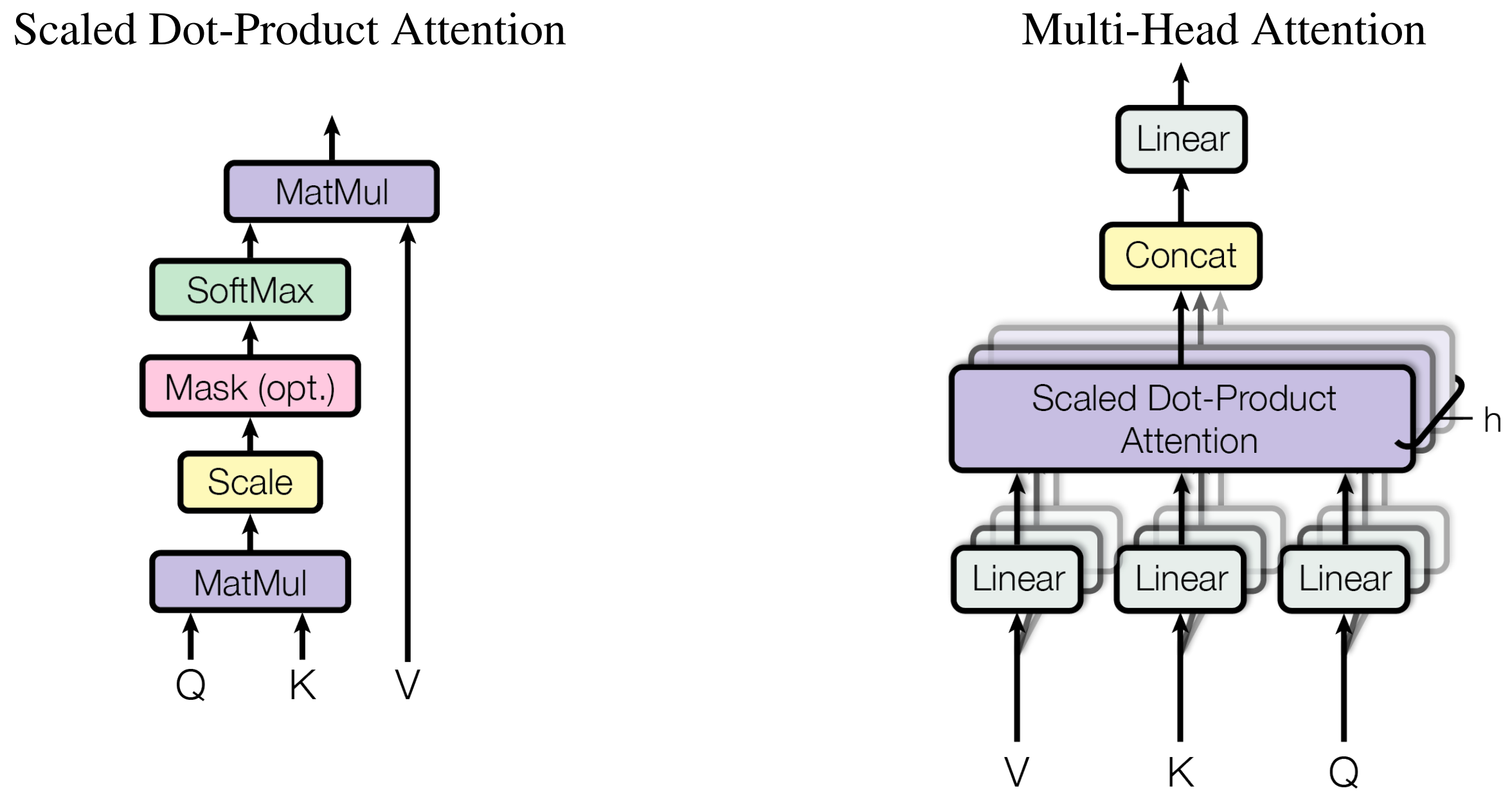
2.3 注意力机制

注意力的核心思想：对每个“查询”找一组“键-值”对，按相似度对值做加权平均，得到输出。直观上，注意力让模型“选择性地关注”输入序列的不同位置。

Scaled Dot-Product Attention（缩放点积注意力）公式： \(\text{Attention}(Q,K,V)=\text{softmax}!\Big(\frac{QK^\top}{\sqrt{d_k}}\Big),V\)

• Q（queries）、K（keys）、V（values）通常是矩阵打包的多条向量。
• 缩放因子 $\sqrt{d_k}$ 防止点积绝对值过大使 softmax 梯度消失。
• 在实现中，若 Q 的形状是 (B, H, L, D)，K 是 (B, H, S, D)，则 scores = Q @ K^T 会得到 (B, H, L, S)，再 softmax 后与 V (B,H,S,D) 矩阵乘得到 (B,H,L,D) 输出。

常见的 mask：

• padding mask：把填充位置的 score 置为很小值，softmax 后权重接近 0。
• causal mask（自回归掩码）：上三角位置设为 -inf，阻止 decoder 看到未来 token。

2.4 多头注意力机制

单个注意力头只能从一个投影子空间里学习依赖关系。多头注意力把 Q/K/V 各自线性投影成 h 组子空间（每组维度更小），并行地在这些子空间上做注意力，再把各头结果拼接、投影回原维度。这样模型能在不同表示子空间并行地捕获不同类型的关系（例如局部语法、长距依赖、词性信息等）。

数学上： \(\text{MultiHead}(Q,K,V) = \text{Concat}(\text{head}_1,\dots,\text{head}*h),W_O\) 其中 $\text{head}i=\text{Attention}(QW^Q_i,KW^K_i,VW^V_i)$。若 $d{model}$ 是模型总维度，通常令每个 head 的维度 $d_k=d_v=d*{model}/h$。

张量维度流程（典型）：

• 输入： x shape = (B, L, d_model)
• 线性映射后 reshape 分头： (B, L, h, d_k) → transpose → (B, h, L, d_k)
• attention → (B, h, L, d_k) → 合并回 (B, L, d_model) → 输出线性映射。

2.5 残差、层规范与前馈网络

每个子层后使用 残差连接（Residual） 和 LayerNorm：x' = LayerNorm(x + Sublayer(x))。

这样能缓解深层网络训练时梯度消失/退化问题。子层间的前馈网络通常是对每个位置独立的两层线性变换 + 非线性（如 ReLU 或 GeLU），形式为：FFN(x) = max(0, x W1 + b1) W2 + b2。

它提升了每位置的非线性表示能力。

3 代码实现

3.1 实现缩放点积注意力函数

核心函数实现：

def scaled_dot_product_attention_simple(
    query: mx.array,
    key: mx.array,
    value: mx.array,
    scale: float | None = None,
    mask: mx.array | None = None,
) -> mx.array:
    scale_factor = scale if scale is not None else 1.0 / mx.sqrt(query.shape[-1])   # scale_factor = 1 / sqrt(d_k)
    scores = mx.matmul(query, key.swapaxes(-2, -1)) * scale_factor # scores = q @ k^T / sqrt(d_k)
    if mask is not None:
        scores  = scores + mask
    scores = mx.matmul(softmax(scores, axis=-1), value)   # scores = softmax(scores) @ v
    return scores

辅助函数 softmax 实现：

def softmax(x: mx.array, axis: int) -> mx.array:
    # softmax(x_i) = exp(x_i) / sum_j exp(x_j)
    x_max = mx.max(x, axis=axis, keepdims=True)
    x_exp = mx.exp(x - x_max)
    x_exp_sum = mx.sum(x_exp, axis=axis, keepdims=True)
    return x_exp / x_exp_sum

3.2 实现多头注意力层

核心函数实现：

class SimpleMultiHeadAttention:
    def __init__(
        self,
        hidden_size: int,
        num_heads: int,
        wq: mx.array,
        wk: mx.array,
        wv: mx.array,
        wo: mx.array,
    ):
        self.d_model = hidden_size
        self.h = num_heads
        assert hidden_size % num_heads == 0
        self.d_k = hidden_size // num_heads
        self.wq = wq
        self.wk = wk
        self.wv = wv
        self.wo = wo


    def __call__(
        self,
        query: mx.array,
        key: mx.array,
        value: mx.array,
        mask: mx.array | None = None,
    ) -> mx.array:
        # 1. liear
        N, L, _ = query.shape   # query: (N, L, d_model)
        query = (
            linear(query, self.wq)  # query: (N, L, d_model)
            .reshape(N, L, self.h, self.d_k)    # query: (N, L, h, d_k)
            .transpose(0, 2, 1, 3)  # query: (N, h, L, d_k)
        )
        key = (
            linear(key, self.wk)
            .reshape(N, L, self.h, self.d_k)
            .transpose(0, 2, 1, 3)
        )
        value = (
            linear(value, self.wv)
            .reshape(N, L, self.h, self.d_k)
            .transpose(0, 2, 1, 3)
        )

        # 2-3. scaled dot-product attention & concat
        scale = 1.0 / mx.sqrt(self.d_k)   # scale = 1 / sqrt(d_k)
        scores = (
            scaled_dot_product_attention_simple(query, key, value, scale, mask=mask)  # scores: (N, h, L, d_k)
            .transpose(0, 2, 1, 3)  # scores: (N, L, h, d_k)
            .reshape(N, L, self.d_model)  # scores: (N, L, d_model)
        )

        # 4. linear
        return linear(scores, self.wo)  # output: (N, L, d_model)

辅助函数 linear 实现：

def linear(
    x: mx.array,
    w: mx.array,
    bias: mx.array | None = None,
) -> mx.array:
    # y = x @ w.T + bias
    # x [N, L, in_features], w.T [in_features, out_features], y [N, L, out_features]
    y = mx.matmul(x, w.T)
    if bias is not None:
        y = y + bias
    return y

4 参考资料

• Tiny-LLM Week1-Day1
• Hugging Face Transformer 模型介绍
• Hugging Face 注意力机制详解
• Hugging Face 编码器-解码器架构
• Hugging Face 注意力掩码机制
• Attention Is All You Need 论文
• 哈佛注解版 Transformer