HDD: Hierarchical Delta Debugging

This is a note for the paper HDD: Hierarchical Delta Debugging.

Abstract

During program debugging, failure-inducing inputs are often large and contain irrelevant information, making debugging more challenging. Simplifying inputs can facilitate debugging. The Delta Debugging algorithm can minimize such inputs, but its efficiency and output quality are limited when handling structured data such as XML.

This paper proposes a new algorithm called HDD (Hierarchical Delta Debugging), specifically designed for tree-structured inputs (e.g., XML). This method processes data layer by layer, enabling early removal of irrelevant parts while ensuring that each generated input configuration remains syntactically valid, thus reducing invalid tests and minimizing overall debugging time.

1. Delta Debugging

1.1 Overview of DD

Delta Debugging (DD) is an automated test case simplification algorithm that aims to find the smallest input subset that causes a program failure, referred to as the “1-minimal test case.” This minimized input set cannot be further reduced while still preserving the failure-inducing property.

The key steps of the DD algorithm include:

1. Subset Reduction: Split the input into n partitions and test each partition. If a partition still induces a failure, treat it as a new input configuration and restart the reduction process.
2. Complement Reduction: Test the complement of each partition. If the complement still induces a failure, treat it as a new input configuration and restart the reduction process.
3. Increase Granularity: Try to split the current input into smaller partitions. If further splitting is impossible, the current configuration is considered 1-minimal, and the algorithm terminates.

The DD mechanism works similarly to a binary search. The goal is to generate partitions of roughly equal size to maximize the chances of removing unnecessary elements. Ideally, each iteration reduces the input size by at least half.

1.2 Limitations of DD

Despite its effectiveness in test case minimization, DD has several limitations:

• Lack of Structural Awareness: DD ignores the input structure, treating it as a flat string or list. When dealing with nested or recursive inputs, this approach may generate many invalid configurations, leading to wasted tests.
• Difficulty Handling Dispersed Failures: Failure-inducing parts may be scattered across different sections of the input file. DD struggles to efficiently locate such dispersed failure causes.

1.3 Improvements in HDD

Hierarchical Delta Debugging (HDD) improves upon the limitations of DD by leveraging the hierarchical structure of input data and performing reduction level by level. Instead of treating the input as a flat sequence, HDD processes it as a tree and operates on whole subtrees. This enables more efficient removal of irrelevant parts and produces simplified test cases.

2. Hierarchical Delta Debugging

2.1 Algorithm Description

HDD focuses on handling hierarchical input data by minimizing configurations level by level, starting from the top. The core idea is to first determine the minimal failure-inducing configuration at the coarsest level, then recursively refine it at finer levels.

Steps of the HDD algorithm:

1. Node Marking and Counting: Before processing each level, the algorithm counts the nodes at that level and assigns a unique identifier to each node. This is achieved by traversing the tree structure and labeling nodes.
2. Applying ddmin: The standard Delta Debugging algorithm (ddmin) is applied to nodes at the current level to minimize the configuration. The testing process determines whether the new configuration still induces a failure.
3. Pruning Irrelevant Nodes: After identifying the minimal configuration at the current level, irrelevant nodes are pruned using a helper function (PRUNE).
4. Proceed to the Next Level: Once the current level is processed, the algorithm moves to the next level in the tree and repeats the process.

2.2 Algorithm Complexity

• Under ideal conditions, the complexity of HDD can be reduced to $O(log⁡n)$.
• In the worst case, the complexity of HDD matches that of DD at $O(n^2)$.

2.3 On Minimality

• DD guarantees 1-Minimality since it reduces input at the finest level of granularity.
• HDD, because it reduces input hierarchically, does not always guarantee 1-Tree-Minimality.
• To achieve 1-Tree-Minimality, two enhanced variants are proposed:
  • HDD+:
    • First applies the standard HDD algorithm to perform greedy pruning.
    • Then performs a BFS-style traversal to remove individual nodes until further reduction is impossible while preserving the failure.
    • Worst-case complexity is $O(n^2)$.
  • HDD*:
    • Invokes HDD multiple times, each time attempting to remove a single node.
    • Continues until no further nodes can be removed without losing the failure.
    • Worst-case complexity is $O(n^3)$.

2.4 Example

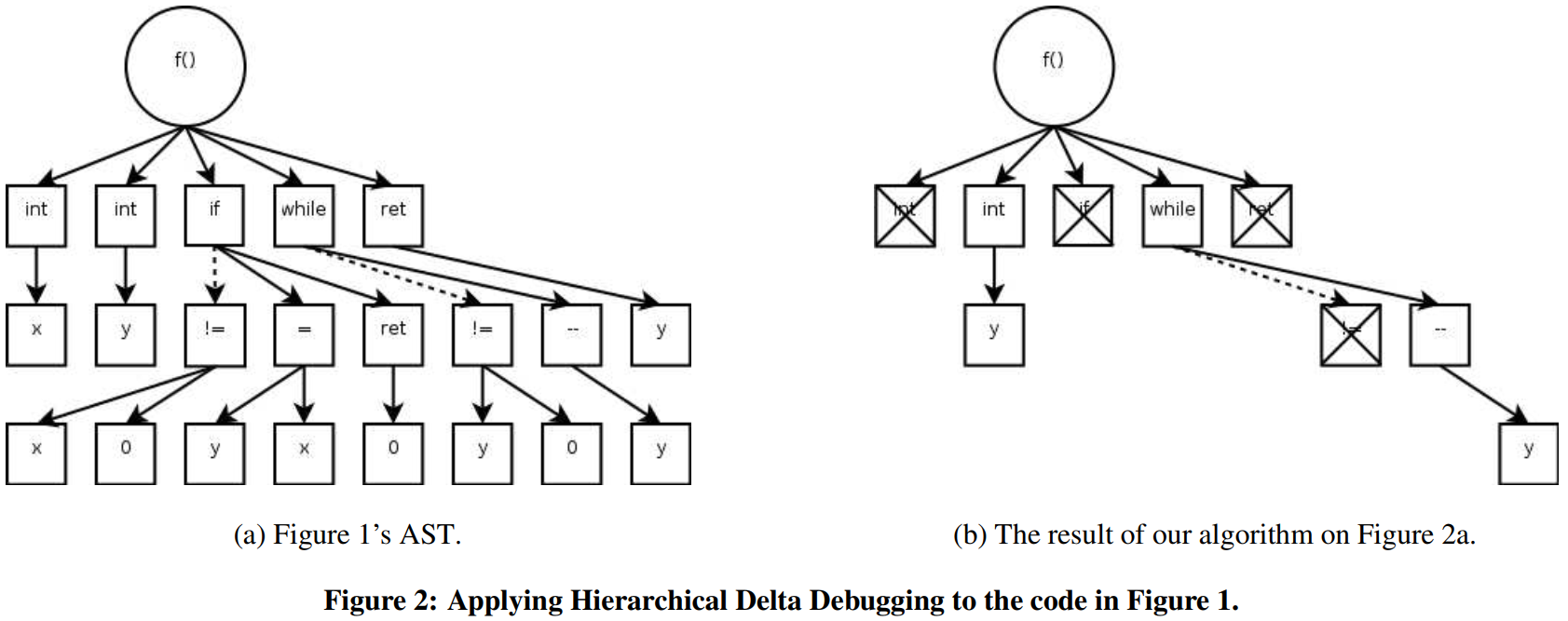
To illustrate the HDD algorithm, consider a simple C program. Suppose the post-decrement operator y-- in function f() causes a compiler failure. The HDD algorithm processes the input as follows:

1. Top-level Processing: Identify the minimal configuration at the top level (e.g., function declarations, global variables). The function f() is necessary to induce the failure and will be retained.
2. Next-Level Processing: Once the top-level configuration is minimized, HDD processes the next level, including function body, statements, and local declarations.
3. Refinement: This process continues level by level until the minimal Abstract Syntax Tree (AST) is obtained.

Original Code:

void f() {
    int x; int y;
    if (x != 0) { y = x; } else { return 0; }
    while (y != 0) { y--; }
    return y;
}

Minimized Code:

f() { int y; while (0) { y--; } }

3. Experiments

• Increased Efficiency: HDD significantly reduces the number of test cases required in all test scenarios, improving debugging efficiency.
• Simplified Output: HDD produces smaller failure-inducing configurations, helping developers locate and understand bugs more quickly.
• Practical Value: Experimental results demonstrate that HDD is more effective and efficient than the original Delta Debugging algorithm when handling structured inputs (e.g., C programs and XML documents).

4. Future Work

1. Current Implementation Limitations:

• Elsa Extension Limitations:
  • Some list types are immutable, preventing expression simplification.
  • Multiple variable declarations in a single statement are split into separate statements.
• Dependency Issues:
  • Excessive dependencies between input levels can limit output minimization.
  • Careful evaluation of the input domain and minimization goals is necessary when using HDD*.
• Manual Tree Processing Dependency:
  • Developers must provide infrastructure for tree processing (e.g., parsing, pruning).
  • XML is easier to handle due to its simple syntax.

2. Potential Algorithm Enhancements:

• Automated Tree Processing with Context-Free Grammars (CFG):
  • A parser could be generated from a CFG to build the input tree and provide basic tree manipulation functions.
  • Nodes could be symmetrically treated to simplify tree operations.
  • Flattening of lists using annotations could reduce recursion depth and improve efficiency.
• Syntax Validity Issues:
  • Generated configurations may be syntactically invalid in some cases (e.g., missing operators).
  • HDD could treat certain symbols as removable nodes and attempt various configurations.
• Optimized ddmin Invocation:
  • ddmin could be applied only to child nodes of a parent rather than the entire level.
  • This would reduce worst-case complexity and improve performance.
  • The algorithm would resemble a breadth-first search (BFS).